Calcular porcentagem online – 100% grátis

Ao longo dos meus anos trabalhando com matemática financeira, percebi que calcular porcentagem é uma das habilidades mais requisitadas no dia a dia. Seja para entender descontos, calcular juros ou analisar variações, dominar esse conceito transforma sua relação com números.

Vou compartilhar minha experiência prática e apresentar ferramentas que uso diariamente para facilitar esses cálculos.

Entendendo o Conceito de Porcentagem

Porcentagem significa “por cem” e representa uma fração de 100. Quando explico esse conceito, sempre deixo claro que 25% é simplesmente 25 divididos por 100, resultando em 0,25.

O sinal de percentagem (%) deve aparecer após o número, com um pequeno espaço entre número e %, embora essa regra seja frequentemente ignorada no uso cotidiano.

Como Calcular Porcentagem: Método Básico

Durante minhas consultorias, desenvolvi um método simples para calcular porcentagem de qualquer valor. A fórmula básica é:

(Valor × Porcentagem) ÷ 100

Por exemplo, para calcular 20% de 500:

• Multiplique 500 × 20 = 10.000
• Divida por 100 = 100
• Resultado: 100

Método Alternativo Mais Rápido

Converta a porcentagem em decimal e multiplique diretamente. Para 20% de 500:

• 20% = 0,20
• 500 × 0,20 = 100

Simulador de Porcentagens: Ferramenta Profissional

Após anos fazendo cálculos manuais, reconheço o valor de uma calculadora de porcentagem online para operações complexas. Por isso, desenvolvi simuladores específicos que uso em meu trabalho diário.

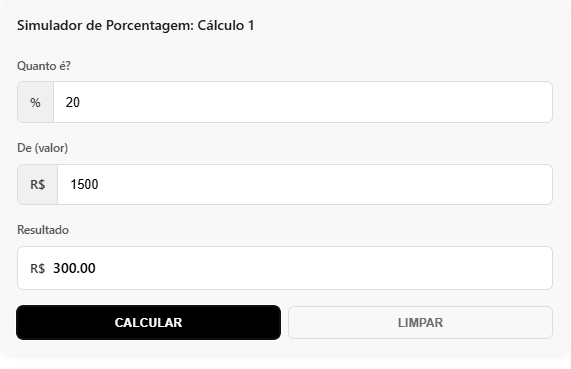
Simulador de Porcentagem: Cálculo 1

Este simulador resolve o cálculo mais comum: descobrir quanto é X% de um valor específico.

Como usar:

• Insira o valor base no campo “Quanto é”
• Digite a porcentagem desejada
• Clique em “CALCULAR”

Exemplo prático: Se você quer saber quanto é 15% de R$ 300, o simulador retorna instantaneamente R$ 45. Uso essa ferramenta frequentemente em reuniões comerciais para calcular descontos rapidamente.

Simulador de Porcentagem: Cálculo 2

Este calcula qual porcentagem um valor representa de outro total.

Aplicação real: Quando preciso saber que porcentagem R$ 80 representa de R$ 400, este simulador mostra 20% imediatamente. Muito útil para análises de participação de mercado ou desempenho de vendas.

A fórmula aplicada é: (Valor ÷ Total) × 100

Simulador de Porcentagem: Cálculo 3

Esta ferramenta descobre o valor original quando você conhece apenas o resultado após aplicar uma porcentagem.

Exemplo de uso: Se um produto custa R$ 120 após 20% de desconto, este simulador calcula o preço original de R$ 150. Essencial para análises de precificação e estratégias comerciais.

Simulador de Porcentagem: Cálculo 4

Este calcula a variação percentual entre dois valores – uma das operações que mais realizo em análises financeiras.

Aplicação prática: Para descobrir o crescimento de um investimento que saiu de R$ 1.000 para R$ 1.300, o simulador mostra 30% de aumento. A fórmula é:

Variação % = [(Valor Final – Valor Inicial) ÷ Valor Inicial] × 100

Fórmulas Percentuais Essenciais

Ao longo da minha carreira, identifiquei três fórmulas percentuais que resolvem 90% dos problemas cotidianos:

1. Calcular X% de um valor: (Valor × X) ÷ 100

2. Descobrir que porcentagem Y é de Z: (Y ÷ Z) × 100

3. Encontrar o valor total: (Valor parcial × 100) ÷ Porcentagem

Cálculos Sem Calculadora: Técnicas Mentais

Aprendi que alguns percentuais são fáceis de calcular mentalmente:

10% – Mova o separador decimal uma casa à esquerda 5% – Calcule 10% e divida por 2 1% – Mova o decimal duas casas à esquerda 25% – Divida o valor por 4

Essas técnicas me salvam constantemente em reuniões. A proporcionalidade direta entre os valores facilita esses cálculos rápidos.

Porcentagem de Desconto e Aumento

No comércio, trabalho frequentemente com descontos e aumentos percentuais.

Calculando Descontos

Para um produto de R$ 200 com 30% de desconto:

• Calcule 30% de 200 = 60
• Subtraia do preço original: 200 – 60 = 140

Método alternativo: Multiplique pelo complemento (100% – 30% = 70%)

• 200 × 0,70 = 140

Calculando Aumentos

O mesmo princípio se aplica ao percentual de aumento, mas somamos. Um produto de R$ 100 com 20% de aumento:

• 100 × 1,20 = 120

Aplicações Financeiras Práticas

Minha experiência com simulador empréstimo e análise financeira ensinou que compreender porcentagens é vital para decisões econômicas inteligentes.

Taxa de Juros e Juros Compostos

Quando avalio propostas de crédito, sempre verifico a taxa de juros real e o Custo Efetivo Total (CET). Os juros compostos fazem a dívida crescer exponencialmente.

A fórmula que uso: Montante = Principal × (1 + taxa)^tempo

IVA e Tributos

O IVA (Imposto sobre Valor Acrescentado) exige cálculo de porcentagem preciso. Se um produto custa R$ 100 mais 15% de IVA, o preço de venda final será R$ 115.

Variação Percentual e Diferença Percentual

Quando analiso dados financeiros, frequentemente preciso calcular a variação percentual entre dois períodos.

Diferença Percentual vs Ponto Percentual

Um ponto percentual representa uma unidade absoluta. Se a inflação subiu de 5% para 8%, houve aumento de 3 pontos percentuais, mas um aumento percentual de 60% (3÷5×100).

Esta distinção é crucial em análises econômicas e políticas públicas.

Conceitos Avançados

Proporcionalidade Direta e Inversa

A proporcionalidade direta facilita cálculos rápidos. Na proporcionalidade inversa, o aumento de uma variável causa diminuição proporcional da outra.

Percentagem Negativa

Ocorre quando há redução no valor original. Um decréscimo de 20% pode ser representado como -20%.

Logaritmos e Diferença Logarítmica

Em análises estatísticas avançadas, uso logaritmos para cálculos de crescimento exponencial. A diferença logarítmica é útil em contextos econométricos específicos.

Ferramentas Complementares

Além dos simuladores de porcentagem, uso frequentemente:

Comparador financeiro – Para avaliar diferentes propostas Tabelas financeiras – Para consultas rápidas Contador digital – Para somatórias complexas

Para cálculos ainda mais específicos, recomendo a Calculadora da Alicia, que oferece recursos adicionais para operações matemáticas diversas.

Média e Desvio Padrão

Em análises estatísticas, combino porcentagens com média e desvio padrão para entender dispersão de dados. O centésimo (cada uma das 100 partes) é fundamental nessas análises.

Minha Metodologia Testada

Após anos ensinando pessoas a calcular porcentagem, desenvolvi uma abordagem que combina teoria e prática.

Primeiro, garanto compreensão do conceito fundamental. Depois, praticamos com exemplos reais. Incentivo cálculos manuais antes de usar ferramentas digitais – isso desenvolve intuição numérica.

Quando uso uma calculadora grátis ou calculadora online, sempre verifico se o resultado faz sentido logicamente.

Dicas Para Dominar Porcentagens

1. Pratique diariamente – Use situações cotidianas como descontos em compras

2. Valide com ferramentas – Compare seus cálculos manuais com simuladores

3. Entenda o contexto – Saiba quando usar cada fórmula

4. Domine o básico – 10%, 25%, 50% devem ser automáticos

Conclusão

Dominar como calcular porcentagem não é dom natural – é habilidade adquirida através da prática consistente. Os métodos e ferramentas que compartilhei foram refinados ao longo de anos trabalhando com educação financeira.

Comece com conceitos básicos, use os simuladores para validar seus cálculos e, gradualmente, avance para situações complexas. Seja calculando o preço original após desconto, entendendo a inflação ou planejando investimentos, essas ferramentas são essenciais.

Use os simuladores acima para praticar diferentes cenários. Sua confiança com números crescerá exponencialmente, assim como sua capacidade de tomar decisões financeiras mais inteligentes.

FAQs